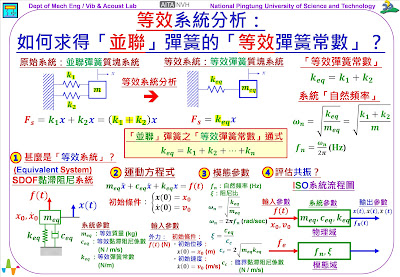
這個單元要來探討的主題是:「等效系統分析」(Equivalent System Analysis),探討如何求得「並聯彈簧」(Parallel springs)的「等效彈簧常數」(Equivalent spring constant) 𝒌𝒆𝒒。
參閱圖示左上方,是一個原始系統:「並聯彈簧」(Parallel springs)的質塊系統,有兩個彈簧分別是
𝒌𝟏 和 𝒌𝟐,以並聯方式和一個質塊 𝒎 連接在一起,此系統的DOF自由度是𝒙(𝒕)。
在此的「等效系統分析」之分析目標,在取得如圖示中間上方的「等效系統」(Equivalent System):單自由度的「等效彈簧質塊系統」,其System 系統參數是:𝒎𝒆𝒒 「等效質量」(Equivalent mass)和 𝒌𝒆𝒒「等效彈簧常數」(Equivalent spring constant)。
完成「等效系統分析」,可以得到「等效系統」可對應等效於原始系統。
要往下討論之前,先回顧前一個單元主題:甚麼是「等效系統」(Equivalent System)?以及為什麼要進行「等效系統分析」(Equivalent System Analysis)?主要意義與目的,參閱圖片的下方系列圖示,說明如下:
1. 當取得了SDOF單自由度系統的「等效系統」(Equivalent System):可取得System 系統參數:就是𝒎𝒆𝒒、𝒄𝒆𝒒、𝒌𝒆𝒒,分別是「等效質量」、「等效黏滯阻尼係數」、「等效彈簧常數」。
2. 推導得到系統的運動方程式(Equation of Motion, EOM):除了System 系統參數以及Output 輸出參數,位移𝒙(𝒕)/速度𝒙 ̇(𝒕)/加速度𝒙 ̈(𝒕),還包括:Input 輸入參數:外力 𝒇(𝒕),和兩個初始條件(IC),𝒙𝟎和𝒗𝟎。
3. 進而可以進行「模態分析」(modal analysis):可以得到「模態參數」(modal parameter):「自然頻率」(natural frequency) 𝒇𝒏 以及「阻尼比」(damping ratio) 𝝃。
4. 評估「共振」(resonance):即可據以評估結構系統是否有「共振」,也就是在比較探討外力 𝒇𝒆「激振頻率」(excitation frequency)和系統的𝒇𝒏「自然頻率」。如果,𝒇𝒆
≅ 𝒇𝒏,就會「共振」,反之,就沒有「共振」。
瞭解了進行「等效系統分析」的意義與目的,主要是不必進行複雜的如「暫態響應分析」(transient response analysis),就可以快速分析判斷結構是否會有「共振」?
再回到原始系統:「並聯彈簧」(Parallel springs)的質塊系統,觀察取得所有彈簧的彈簧力𝑭𝒔,可得到:𝑭𝒔 = 𝒌𝟏 𝒙 + 𝒌𝟐 𝒙 = (𝒌𝟏+𝒌𝟐) 𝒙。
另外,由「等效系統」:單自由度的「等效彈簧質塊系統」,觀察取得「等效彈簧」的彈簧力𝑭𝒔,可得到:𝑭𝒔 = 𝒌𝒆𝒒 𝒙。
比較原始系統和「等效系統」的彈簧力𝑭𝒔方程式,可以得到「並聯彈簧」的「等效彈簧常數」𝒌𝒆𝒒
= 𝒌𝟏+𝒌𝟐。
其次,即可帶入
𝒇𝒏 方程式,如果,已知:𝒎𝒆𝒒、𝒌𝒆𝒒,即可求得系統的 𝒇𝒏「自然頻率」。在此系統,𝒎𝒆𝒒 = 𝒎,所以,可明確求得系統的 𝒇𝒏。
最後,由於取得了系統的
𝒇𝒏「自然頻率」,可以和 𝒇𝒆「激振頻率」比較探討。如果,𝒇𝒆
≅ 𝒇𝒏,就會「共振」,反之,就沒有「共振」。
同理,可以推導出「並聯彈簧」的 𝒌𝒆𝒒「等效彈簧常數」通式:𝒌𝒆𝒒 = 𝒌𝟏+𝒌𝟐+…+𝒌𝒏,共有𝒏個「並聯彈簧」。
綜合這個單元的討論,進行的是「等效系統分析」(Equivalent System Analysis),探討如何求得「並聯彈簧」(Parallel springs)的「等效彈簧常數」(Equivalent spring constant) 𝒌𝒆𝒒。進而,可以取得了系統的
𝒇𝒏「自然頻率」,再和 𝒇𝒆「激振頻率」比較,可以評估「共振」(resonance)。如果,𝒇𝒆 ≅ 𝒇𝒏,就會「共振」,反之,就沒有「共振」。
以上個人看法,請多指教!
王栢村
2023.06.30














0 意見:
張貼留言