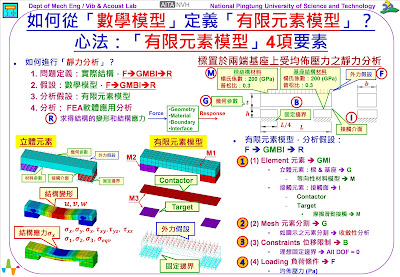
這個單元要來探討的主題是:如何從「數學模型」(Mathematical Model)定義「有限元素模型」(Finite Element Model, FE Model)?需要的心法:是「有限元素模型」4項要素。
在先前單元:#289,【如何進行結構的「靜力分析」?】,探討如何進行「靜力分析」,主要步驟,包括:
1. 定義問題:
2. 建構數學模型:
3. 發展有限元素模型:
4. 進行FEA軟體應用分析:
5. 解讀分析結果討論評估:
其中,第三個步驟,就是要建構「有限元素模型」(FE Model),本單元將應用「有限元素模型」4項要素的心法,來思考如何從「數學模型」定義「有限元素模型」。
快速回顧一下,如何進行「靜力分析」,主要步驟,包括:
1. 「問題定義」(Problem Definition):就是對「實際結構」(Real Structure)有明確的定義問題,在先前單元:#295,【針對「靜力分析」,如何「定義問題」?心法:FGMBIR】,就是採用【F → GMBI → R】心法,對結構的「靜力分析」做問題定義,也就是以【Input → System → Output】=【ISO】,做系統化的「定義問題」。
2. 「假設」(Assumptions):透過適當的分析假設,建構「數學模型」(Mathematical Model),在先前單元:#296,【如何從「實際結構」定義「數學模型」 ?心法:FGMBIR】,也是應用【F → GMBI → R】心法,從「實際結構」(Real Structure)定義「數學模型」(Mathematical Model)。
3. 「分析假設」(Analysis Assumptions):當採用有限元素分析(Finite Element Analysis, FEA)軟體,進行分析時,就需要建構對應的「有限元素模型」(Finite Element Model, FE Model)。 當有了「數學模型」,就要明確的定義「有限元素模型」,就是這個單元討論的重點。
4. 「分析」(Analysis):應用FEA軟體進行結構分析,就可以求得結構的變形(deformation)和結構應力(stress)。
接續前兩個單元:#295,【針對「靜力分析」,如何「定義問題」?心法:FGMBIR】,以及#296,【如何從「實際結構」定義「數學模型」 ?心法:FGMBIR】,所探討的結構案例:樑置於兩端基座上受均佈壓力之靜力分析,參閱圖示右上方的示意圖,說明如下:
1. 已經應用【F → GMBI → R】心法,完成了「實際結構」的「問題定義」(Problem Definition)。
2. 也是應用【F → GMBI → R】心法,完成了「實際結構」(Real Structure)定義「數學模型」(Mathematical Model)。
當採用「立體元素」時,參閱圖示左下方的三個圖示,分別是:
1. 採用「立體元素」的「有限元素模型」示意圖:分別標示了Force外力、Geometry幾何、Material材料、Boundary邊界條件、Interface接觸介面。也就是【F → GMBI】。
2. 結構的變形(deformation)分布圖:可以得到三個方向的結構變形位移參數(𝒖, 𝒗, 𝒘)。
3. 結構的應力(stress) 分布圖:可以得到3個方向的正向應力Normal stress (𝝈𝒙,𝝈𝒚,𝝈𝒛)和3個方向的剪應力Shear
stress
(𝝉𝒙𝒚,𝝉𝒚𝒛, 𝝉𝒙𝒛),因此,可以取得3個主應力Principal stress (𝝈𝟏,𝝈𝟐,𝝈𝟑)以及等效應力Equivalent/Effective stress,也稱為von Mises
stress麥西斯應力(𝝈𝒆𝒒𝒗)。
要能夠得到如上說明的分析結果,只有「數學模型」是不夠的,仍需要建構發展對應的「有限元素模型」,才能夠進入到FEA軟體進行結構分析,實現所擬進行的分析構想。
要建構「有限元素模型」(FE Model),需要的心法是「有限元素模型」4項要素,其對應【F → GMBI → R】心法,如下:
1. Element 元素 → GMI
2. Mesh 元素分割
→ GM
3. Constraints 位移限制 → B
4. Loading 負荷條件 → F
參閱圖示中間下方的圖示,為本案例的「有限元素模型」示意圖。首先,針對要素(1) Element 元素,說明如下:
1. 「立體元素」(solid element):在「數學模型」已經設定選擇是採用「立體元素」,所以對樑結構和基座結構的Geometry幾何,都以「立體元素」建構。須注意,要分別給定樑M1和基座M2對應的Material材料參數(Material parameters),最簡單的材料模型,就是「等向性材料模型」(Isotropic Material Model),需要定義楊氏係數(Young’s modulus):200 (GPa),普松比(Poisson ratio):0.3,是典型的鋼材。如果,基座是木材,就可設定為木材的材料參數。
2. 「接觸元素對」(contact element pair):因為採用「立體元素」,在樑與基座的Interface接觸介面是面對面的接觸(face-to-face contact)。接觸元素是成對的,通常會定義接觸面(Contactor)和被接觸面(Target),係以力傳遞的概念來設定,由於力的傳遞是由上而下,所以,樑結構的底面就是Contactor,而兩個基座的頂面就是Target。在此,樑結構是置放在基座的上方,所以,可以合理的假設,此Interface接觸介面是「摩擦滑動接觸」(frictional sliding contact)。所以,需要設定「接觸元素對」材料參數M3,如「摩擦係數」(frictional coefficient)。
在要素(1) Element 元素,就是要對結構所有的零組件Geometry幾何,定義所採用的對應元素型式,同時,定義其Material材料參數。也要界定Interface接觸介面的接觸狀態,以及所需要「接觸元素對」及其Material材料參數。所以要素(1) Element 元素,對應的是GMI。
其次,針對要素(2) Mesh 元素分割,就是選擇適當的分割元素的大小,在對結構分割元素(meshing)時,需要注意,不同的零組件,可能有不同的Material材料參數。所以要素(2) Mesh 元素分割,對應的是GM。
另外須注意Mesh 元素分割時,當然要進行必要的「收斂性分析」(convergence analysis),以確認分析的準確性。可參考先前單元:#293,【甚麼是「收斂性分析」?】。
針對要素(3) Constraints 位移限制,就是對應於Boundary邊界條件,在此假設基座底部是理想狀態的固定邊界(ideally fixed
boundary),所以基座底部的所有節點(node)的自由度(degree of freedom, DOF)都為零,也就是三個方向的位移(𝒖, 𝒗, 𝒘)=(0, 0,
0)。所以要素(3) Constraints 位移限制,對應的是B。
最後,針對要素(4) Loading 負荷條件,就是對應於Force外力,在本案例是作用於樑結構頂部表面的均佈下壓力(Pa)。所以要素(4) Loading 負荷條件,對應的是F。
最後綜合一下本單元的討論,係針對進行「靜力分析」的第三個步驟,要建構「有限元素模型」(FE Model),應用「有限元素模型」4項要素的心法,來思考如何從「數學模型」定義「有限元素模型」,使得能夠在進入到FEA軟體進行結構分析時,實現所擬進行的分析構想。
要建構「有限元素模型」(FE Model),需要的心法是「有限元素模型」4項要素,其對應【F → GMBI → R】心法,再次彙整如下:
1. Element 元素 → GMI
2. Mesh 元素分割
→ GM
3. Constraints 位移限制 → B
4. Loading 負荷條件 → F
以上個人看法,請多指教!
王栢村
2022.11.28