這個單元要來探討的主題是:甚麼是「收斂性分析」(convergence analysis)?在採用「有限元素分析」(Finite Element Analysis, FEA)時,「收斂性分析」是一項重要的技術。
首先,以「4W」的心法,來破題、討論「收斂性分析」(convergence analysis)如下:
1.
What is? 甚麼是「收斂性分析」?
2.
Why to do? 為什麼需要進行「收斂性分析」?
3.
What goals? 進行「收斂性分析」要達到甚麼目標?
4.
How to do? 如何進行「收斂性分析」?
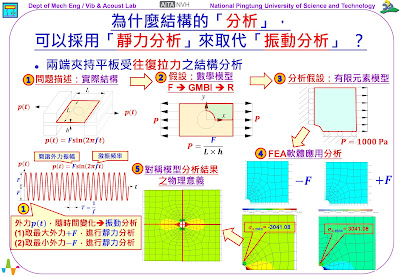
首先,參閱圖示右邊上方圖示順序,回顧前一個單元的案例:兩端夾持平板受往復拉力之結構分析,係以「靜力分析」方式,進行整體的分析步驟,簡述如下:
1. 定義問題:針對實際結構,在平板兩端有治具的夾持,夾持位置兩端受到往復拉力𝒑(𝒕)=𝑭𝐬𝐢𝐧(𝟐𝝅𝒇𝒕)的作用,看起來是一個正弦波的變動外力。
2. 建構數學模型:對實際結構進行適當的分析假設,建議以【F → GBMI → R】心法思考,可以得到對應的「數學模型」(Mathematical Model)。
3. 發展有限元素模型:其次,就要建構對應的「有限元素模型」(finite element model),由於符合結構的「對稱性」,只取1/4個平板進行分析。
4. 進行FEA軟體應用分析:可以應用CAE/FEA有限元素分析軟體進行應用分析,實現出FEA的「有限元素模型」分析構想,圖示為結構應力𝝈𝒙分佈圖,也就是x-方向正向應力分佈圖。
5. 解讀分析結果討論評估:由於採用了1/4個平板的「對稱模型」進行分析,所以,可以以映射方式,取得整體平板的應力分佈,可便於解讀此「對稱模型」應力分佈的物理意義。同時,可觀察出最大、最小應力的發生位置以及其量值大小。
當看到彩色的結構應力𝝈𝒙分佈圖,是否會懷疑這個分析結果的正確性、準確性如何呢?這就需要這個單元,所要討論的「收斂性分析」(convergence analysis)!
首先,What is? 甚麼是「收斂性分析」?最主要是:評估FEA「有限元素分析」之準確性,尤其是「有限元素模型」是層層的分析假設與FEA軟體應用分析的結果,參閱圖示中央的整體平板的應力分佈圖,討論如下:
1. 應力等高線,有尖銳角度:如圖示標註的黑色線段。
2. 應力等高線,是非平滑曲線:結構的變形應該是連續的,如果,應力等高線是非平滑曲線,代表結構呈現了不連續的應力狀態,這是不合理的現象。
由於,有【應力等高線是非平滑曲線】的不合理現象,又,圖示中個格線方塊,代表的就是每一個元素的分割狀態。又,已知元素越小,FEA「有限元素分析」之分析結果就越準。所以,為什麼需要進行「收斂性分析」呢?就是要找到適當的「元素分割」(Mesh),使得有準確的分析結果。題外話:坊間許多人稱之為「網格」是一種以訛傳訛的說法,Mesh真實的物理意義是「元素分割」Mesh的狀態。
所以,進行「收斂性分析」要達到甚麼目標呢?就是要確保FEA分析的準確性。
至於要如何進行「收斂性分析」呢?本單元將介紹「h-收斂性分析」(h-convergence),其中,h代表元素大小的變數符號。以步驟4下方的分析模型圖示,可觀察到:在靠近圓孔附近的「元素分割」尺寸較小,遠離應力集中區域的「元素分割」尺寸較大,這是合理的「元素分割」(Mesh)原則。
如何進行「h-收斂性分析」呢?參閱圖示下方,有5個不同元素尺寸的「有限元素模型」之分析結果,由右至左,係由「粗分割」(coarse mesh)、逐漸「細分割」(refined mesh),每一個「細分割」分別是初始模型之元素尺寸的1/2、1/3、1/4、1/5,圖中分別標示了最小應力𝝈𝒙,𝐦𝐢𝐧之發生位置及量值,不同「元素分割」的最小應力𝝈𝒙,𝐦𝐢𝐧值,也彙整如中間表格。觀察的現象,討論如下:
1. 最小應力𝝈𝒙,𝐦𝐢𝐧之發生位置,都在圓孔的正上方。顯示各個「細分割」模型的合理性。
2. 在最左邊的圖示,「元素分割」尺寸最小,可以觀察:所有的應力等高線都是平滑曲線,所以,沒有結構的不連續應力分布狀態,是合理、良好的物理現象。
3. 參閱表格的𝝈𝒙,𝐦𝐢𝐧數值比較,「細分割」與「粗分割」的「有限元素模型」,其分析結果的相對誤差,都在0.3 %以下。在模型5和4的比較,誤差最小是0.041%。這是合理的「h-收斂性分析」結果。
對這個案例來說,最小應力𝝈𝒙,𝐦𝐢𝐧值,在不同「元素分割」尺寸的分析結果,很相近。不過,可以觀察模型5的應力等高線,在對稱邊界上,呈現鉛錘的直角現象,在鏡像映射後,可以得到平滑曲線,所以模型5,可以說是進行「h-收斂性分析」後,確認的、適當的「元素分割」(Mesh)。
另外,簡要地以最小應力數值來看,與所受到的壓應力,比值大約等於3,可以看出有「應力集中」(stress concentration)現象。更明確的「應力集中係數/因子」(stress concentration factor)定義,我們另闢單元討論。
最後,綜合一下這個單元有關「收斂性分析」(convergence analysis)的討論,是以「4W」的心法來討論:
1.
What is? 甚麼是「收斂性分析」?
2.
Why to do? 為什麼需要進行「收斂性分析」?
3.
What goals? 進行「收斂性分析」要達到甚麼目標?
4.
How to do? 如何進行「收斂性分析」?
以上個人看法,請多指教!
王栢村