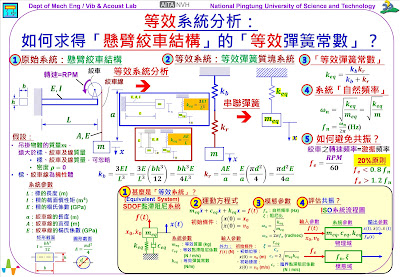
這個單元要來探討的主題是:「等效系統分析」(Equivalent System Analysis),探討如何求得「懸臂絞車結構」的「等效彈簧常數」(Equivalent spring
constant) 𝒌𝒆𝒒。
參閱圖示左上方,是一個原始系統:「懸臂絞車結構」系統。此結構有一個支撐架,相當於是一個懸臂樑,在樑的自由端有絞車,絞車線下方有一個吊掛物體,其質量為𝒎。絞車會有馬達帶動運轉,其轉速RPM,就是每分鐘轉速(revolution per minute, RPM)。絞車馬達運轉在吊載物體時,物體質塊𝒎,會有上下振動,令其DOF自由度是𝒙(𝒕)。
如果,要分析此系統物體質塊𝒎的
𝒙(𝒕) 振動情形,牽涉到複雜的、進階的連續系統(continuous system)分析,在此介紹「等效系統分析」的理念,如圖示中間上方,將以SDOF單自由度的「等效系統」(Equivalent System)來分析,其System 系統參數是:𝒎𝒆𝒒 「等效質量」(Equivalent mass)和 𝒌𝒆𝒒「等效彈簧常數」(Equivalent spring constant)。
由原始系統和「等效系統」的DOF自由度比較,可以判斷:𝒎𝒆𝒒 = 𝒎,所以,接下來的問題,就是如何求得𝒌𝒆𝒒「等效彈簧常數」。
要往下討論之前,先回顧先前單元主題:甚麼是「等效系統」(Equivalent System)?以及為什麼要進行「等效系統分析」(Equivalent System Analysis)?主要意義與目的,參閱圖片的下方系列圖示,說明如下:
1. 當取得了SDOF單自由度系統的「等效系統」(Equivalent System):可取得System 系統參數:就是𝒎𝒆𝒒、𝒄𝒆𝒒、𝒌𝒆𝒒,分別是「等效質量」、「等效黏滯阻尼係數」、「等效彈簧常數」。
2. 推導得到系統的運動方程式(Equation of Motion, EOM):除了System 系統參數以及Output 輸出參數,位移𝒙(𝒕)/速度𝒙 ̇(𝒕)/加速度𝒙 ̈(𝒕),還包括:Input 輸入參數:外力 𝒇(𝒕),和兩個初始條件(IC),𝒙𝟎和𝒗𝟎。
3. 進而可以進行「模態分析」(modal analysis):可以得到「模態參數」(modal parameter):「自然頻率」(natural frequency) 𝒇𝒏 以及「阻尼比」(damping ratio) 𝝃。
4. 評估「共振」(resonance):即可據以評估結構系統是否有「共振」,也就是在比較探討外力 𝒇𝒆「激振頻率」(excitation frequency)和系統的𝒇𝒏「自然頻率」。如果,𝒇𝒆
≅ 𝒇𝒏,就會「共振」,反之,就沒有「共振」。
瞭解了進行「等效系統分析」的意義與目的,再回到原始系統:「懸臂絞車結構」系統,主要是不必進行複雜的、進階的連續系統(continuous system)分析,就可以快速分析判斷結構是否會有「共振」?
原始系統:「懸臂絞車結構」系統。支撐架懸臂樑的結構參數,包括:𝑳:樑的長度 (m),𝑰 :樑的截面慣性矩 (𝐦^𝟒),𝑬:樑的楊氏係數 (GPa)。懸臂樑是矩形截面,所以,截面慣性矩:𝑰=(𝒃𝒉^𝟑)/𝟏𝟐。絞車線的參數,包括:𝒂:絞車線的長度 (m),𝑨:絞車線的直徑 (m),𝑬:絞車線的楊氏係數 (GPa)。絞車線是圓形截面,其截面積:𝑨 =(𝝅𝒅^𝟐)/𝟒。
其次,要進行「等效系統分析」,必須對原始系統做了假設(assumptions),說明如下:
1. 吊掛物體的質量𝒎,遠大於懸臂樑、絞車及線質量,所以,懸臂樑、絞車及線的質量,可忽略,其密度 𝝆= 0。
2. 懸臂樑、絞車線會變形,是撓性體(flexible body),也就是彈性體(elastic body),都需要定義其𝑬:楊氏係數。
瞭解了「懸臂絞車結構」的系統參數,要進行「等效系統分析」,先回顧先前單元,參閱圖示中間上方的兩個示意圖,分別是「懸臂樑」(cantilever beam)以及「懸臂柱」(cantilever column)的「等效彈簧常數」𝒌𝒆𝒒,彙整如下:
1. 「懸臂樑」的「等效彈簧常數」:𝒌𝒆𝒒=𝑭/𝜹 =𝟑𝑬𝑰/𝑳^𝟑。
2. 「懸臂柱」的「等效彈簧常數」:𝒌𝒆𝒒=𝑭/𝜹 =𝑨𝑬/𝑳。
再觀察「懸臂絞車結構」系統,其支撐架的 𝒌𝒆𝒒,相當於一個懸臂樑的
𝒌𝒆𝒒,在此以𝒌𝒃表示,而絞車線的
𝒌𝒆𝒒,相當於「懸臂柱」的 𝒌𝒆𝒒,在此以
𝒌𝒓表示。再參閱圖示中央的兩個彈簧 𝒌𝒃 和 𝒌𝒓,是串聯彈簧質塊系統示意圖,就是原始系統:「懸臂絞車結構」的第一層次的「等效系統」。
在此要注意的是,𝒌𝒃 和
𝒌𝒓 兩個彈簧的連接點位置,就是絞車位置。系統的假設:忽略了絞車質量,如果必須考慮了絞車質量,那麼這個「等效系統」就會是個兩個自由度系統。
接下來,就分別取得𝒌𝒃 和
𝒌𝒓 兩個彈簧的「等效彈簧常數」:
1. 「懸臂樑」的「等效彈簧常數」:𝒌𝒃=𝟑𝑬𝑰/𝑳^𝟑
=𝟑𝑬/𝑳^𝟑
((𝒃𝒉^𝟑)/𝟏𝟐)=(𝒃𝒉^𝟑
𝑬)/(𝟒𝑳^𝟑 )。
2. 「懸臂柱」的「等效彈簧常數」:𝒌𝒓 =𝑨𝑬/𝒂=𝑬/𝒂 ((𝝅𝒅^𝟐)/𝟒)=(𝝅𝒅^𝟐
𝑬)/𝟒𝒂。
接著,因為
𝒌𝒃 和 𝒌𝒓 兩個彈簧是串聯,由先前單元「串聯彈簧」的「等效彈簧常數」,可知:𝒌𝒆𝒒 =(𝒌𝒃 𝒌𝒓)/( 𝒌𝒃+ 𝒌𝒓 )。所以,就可以取得原始系統:「懸臂絞車結構」的「等效彈簧常數」𝒌𝒆𝒒。
其次,即可帶入
𝒇𝒏 方程式,如果,已知:𝒎𝒆𝒒、𝒌𝒆𝒒,即可求得系統的 𝒇𝒏「自然頻率」。在此系統,𝒎𝒆𝒒 = 𝒎,所以,可明確求得系統的 𝒇𝒏。
最後,就是要來評估如何避免「共振」(resonance):也就是系統的外力𝒇𝒆「激振頻率」(excitation frequency)和系統的𝒇𝒏「自然頻率」(natural frequency),𝒇𝒆 ≅ 𝒇𝒏 相等或相近時,會使得結構有大的振動。所以,結構有「共振」的現象,通常是不好的,需要去避免「共振」。反之,就沒有「共振」。
針對原始系統:「懸臂絞車結構」,其系統的外力𝒇𝒆「激振頻率」就是絞車馬達的「轉速頻率」,所以,𝒇𝒆=𝑹𝑷𝑴/𝟔𝟎,單位:Hz。
如前述,要避免「共振」,系統的外力 𝒇𝒆「激振頻率」必須遠離系統的 𝒇𝒏「自然頻率」。一般避免「共振」(resonance)的建議,採20%原則,也就是:𝒇𝒆 < 𝟎.𝟖 𝒇𝒏,或 𝒇𝒆 > 𝟏.𝟐 𝒇𝒏。
所以,對「懸臂絞車結構」的設計,除了由結構靜力分析,分析結構的強度與安全性外,也需要考慮結構振動的動態響應設計,最基本的考慮就是:避免「共振」(resonance)。
綜合這個單元的討論,進行的是「等效系統分析」(Equivalent System Analysis),探討如何求得「懸臂柱」(cantilever column)的「等效彈簧常數」(Equivalent spring constant) 𝒌𝒆𝒒。統整的分析流程步驟理念如下:
1. 探討原始系統:「懸臂絞車結構」系統。
2. 進行「等效系統分析」:定義「等效系統」的單自由度「等效彈簧質塊系統」,其System 系統參數是:𝒎𝒆𝒒 「等效質量」和 𝒌𝒆𝒒「等效彈簧常數」。過程中,有引用了「懸臂樑」和「懸臂柱」以及「串聯彈簧」的「等效彈簧常數」𝒌𝒆𝒒。
3. 分析得到「等效彈簧常數」𝒌𝒆𝒒 以及 𝒎𝒆𝒒 「等效質量」。
4. 進而,可以推算系統的
𝒇𝒏「自然頻率」。
5. 評估「共振」(resonance):系統的 𝒇𝒏「自然頻率」再和 𝒇𝒆「激振頻率」比較,可以評估「共振」(resonance)。如果,𝒇𝒆 ≅ 𝒇𝒏,就會「共振」,反之,就沒有「共振」。建議採用:20%原則,也就是:𝒇𝒆 < 𝟎.𝟖 𝒇𝒏,或 𝒇𝒆 > 𝟏.𝟐 𝒇𝒏。
以上個人看法,請多指教!
王栢村