「阻尼」(damping)是重要的物理現象,這個單元,就來討論一下,甚麼是「阻尼」?
首先,由圖示實體結構的「質塊-彈簧系統」,假設「質塊」吊掛在「彈簧」的下方,如果,對這個質塊往下拉一個距離,然後釋放開質塊,當然,質塊會來回的振盪,如圖示(A)、(B)、(C)三種振盪的狀態:
1.
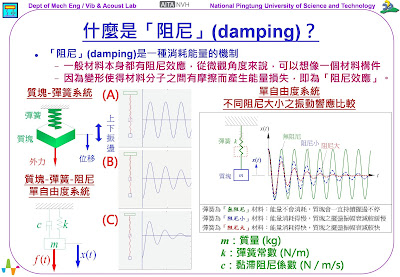
(A)狀態:質塊呈現來回振盪,完全沒有衰減的現象,也就是質塊來回不停歇的振盪。
2.
(B)狀態:質塊在來回振盪時,每一個來回振盪,質塊的振盪幅度,逐漸變小,可以預期,質塊最後將趨近於不振盪的靜止狀態。
3.
(C)狀態:此狀態與(B)相似,不過呢,質塊的振盪幅度,衰減的速度比(B)狀態,還要快,可以預期,質塊比較快趨近於不振盪的靜止狀態。
在這裡,請讀者猜看看,「質塊」的振盪狀態,會是以上(A)、(B)、(C)三種振盪狀態的哪一種呢?提出一些思考討論如下:
1.
因為,有空氣阻力:質塊會受到空氣阻力的效應,所以,會是(B)或(C)的振盪狀態。
2.
如果,質塊-彈簧系統是在水中:質塊在水中,受到的阻力,會更大,因此,(B)可能是在空氣中振盪狀態,而(C)就是在水中的振盪狀態。
3.
如果,在真空狀態:當沒有空氣或水的阻力,質塊的振盪,是否就是(A)狀態,來回振盪的不停呢?為免誤導,在此先說明,不是的,就算在真空中,質塊的來回振盪,也是會逐漸衰減其振盪幅度,最後,還是會趨近於不振盪的靜止狀態。
以上由「阻力」的角度,分別從「在空氣中」、「在水中」、及「在真空中」來看「質塊」的運動振盪狀態,是很好的思考出發點。
甚麼是「阻尼」(damping)?簡單的說:「阻尼」(damping)是一種消耗能量的機制。一般材料本身都有「阻尼效應」。從「微觀」角度來說,可以想像一個材料構件,因為結構體的變形,使得材料分子之間有摩擦,而產生磨擦的能量損失,即為「阻尼效應」。
在此「質塊-彈簧系統」,質塊往下拉伸的來回振盪運動行為,可以討論如下:
1.
質塊是剛體(rigid body):雖然實際物理界,沒有真正的「剛體」,【剛體:結構物體本身不會有變形】。在此,質塊和彈簧的相對運動狀態來說,質塊可以說是接近「剛體」狀態,所以,質塊是剛體,是合理的假設。
2.
彈簧是撓性體(flexible body)或彈性體(elastic body):彈簧受到拉伸及壓縮的效應,彈簧就會有變形,因此,會有前述彈簧材料分子間的摩擦能量損失,而有「阻尼效應」。
3.
不同材料的「阻尼效應」:不同材料最明顯的對比,就是鋼鐵材料和橡膠材料的對比,可以推測鋼材的「阻尼效應」會比橡膠材料,來得小。
另外,再深入思考一下,「空氣阻力」有那麼大的「阻尼效應」嗎?可以知道,如果質塊是個小物體,空氣的阻力效應,其實很小,甚至是可忽略了。所以,質塊來回振盪的衰減現象,主要是來自彈簧材料的「阻尼效應」。在圖示的(B)及(C)的振盪狀態,(B)是彈簧材料的「阻尼效應」小,而(C)是彈簧材料的「阻尼效應」較大。
為了探討這個「質塊-彈簧系統」,可以建構對應此系統的「數學模型」,如圖示的「m、c、k」,「質塊-阻尼-彈簧單自由度系統」,說明如下:
1.
質塊(mass):假設質塊為剛體(rigid body),以一個質點「質量」m,代表質塊,SI制單位:kg。
2.
彈簧(spring):彈簧以其「彈簧常數」(spring
constant),k,代表此彈簧的剛性(stiffness),SI制單位:N/m,是彈簧每單位長度變形的受力。也就是彈簧力fs = k*x,其中,x是質塊的位移變形量,「彈簧力」fs與x成正比。在相同x位移時,k值,越大,彈簧力fs,就越大。
3.
阻尼元件(damper):為了模擬彈簧的「阻尼效應」,常採用的「阻尼模型」(damping model)是「黏滯阻尼模型」(viscous damping model),以「黏滯阻尼係數」(viscous damping coefficient),c,代表此彈簧的「阻尼效應」,SI制單位:N / m/s = N.s/m,是彈簧變形每單位速度的受力,也就是「彈簧阻尼力」fd=c*v。其中,v是質塊的速度,對質塊位移x取一次微分,可以得到質塊的速度v。作用在質塊的阻尼力(damping force) fd,和質塊速度v,成正比。「黏滯阻尼係數」c越大,「阻尼效應」越大。
如果,由mck「質塊-阻尼-彈簧單自由度系統」來看,特別是以「黏滯阻尼係數」c,可以解讀(A)、(B)、(C)三種振盪狀態的差異:
1.
(A)狀態,彈簧無阻尼效應,c=0:實務上,彈簧材料都會有「阻尼效應」,c=0,是數學分析上的假設,可以理解無阻尼時,質塊的振盪現象,是永無止境的來回振盪。
2.
(B)狀態,彈簧有阻尼,c較小:實務上,由於彈簧材料有「阻尼效應」,當c值小時,阻尼效應小,所以,質塊來回振盪的振幅衰減效應,比較慢。
3.
(C)狀態,彈簧有阻尼,c較大:當彈簧材料的「阻尼效應」大,也就是c值較大時,阻尼效應較大,所以,質塊來回振盪的振幅衰減效應,就相對比較快。
由圖示「無阻尼」、「阻尼小」、及「阻尼大」的質塊位移x(t)時間域波形,除了可以看出質塊來回振盪之位移振幅的不同衰減效應。同時,也可以觀察到,來回振盪的「週期」似乎是相同的,這個現象與單自由度系統的「自然頻率」相關,我們再另闢單元討論。
在結束這個單元,為方便讀者查詢,彙整一下有關阻尼的中英文名詞對照:
l
阻尼(damping)
l
阻尼效應(damping effect)
l
阻尼元件、阻尼器(damper)
l
阻尼模型(damping model)
l
黏滯阻尼模型(viscous
damping model, viscously damped model)
l
黏滯阻尼係數(viscous
damping coefficient)
l
阻尼力(damping force)
這個單元以一個「質塊」吊掛在「彈簧」的下方,對這個「質塊」往下拉一個距離,然後釋放開質塊,由質塊會來回的振盪現象,探討說明甚麼是「阻尼」(damping)?並以mck「質塊-阻尼-彈簧單自由度系統」,特別是以「黏滯阻尼模型」(viscous damping model),也就是「黏滯阻尼係數」(viscous damping coefficient),c,代表此彈簧的「阻尼」(damping),了解c值大小之影響與差異。希望由本單元的探討,讀者能夠進一步了解「阻尼」的現象與意義。
以上個人看法,請多指教!
王栢村
2019.07.01