這個單元要來探討的主題是:「庫倫阻尼」(Coulomb Damping)
SDOF系統之暫態響應分析,可以得到甚麼結果?這是「庫倫阻尼」系列的第4篇。
首先,針對這個單元主題的關鍵詞,依序說明:
1. 「庫倫阻尼」(Coulomb Damping) SDOF系統:參閱圖示左下方的系統示意圖,可知系統參數包括:𝒎=質量 (kg),𝒄=黏滯阻尼係數 (N /
m/s),𝒌=彈簧常數 (N/m),𝝁=摩擦係數。
2. 「暫態響應分析」(Transient Response Analysis):主要目的就是要分析取得質塊的時間波形響應,以及各種外力的時間波形響應。
為了要求解「暫態響應分析」,必須推導得到「庫倫阻尼」SDOF系統的運動方程式(Equation of Motion, EOM),其通式如下:𝒎𝒂+𝒄𝒗+𝒌𝒙=𝒇(𝒕)+𝑭𝒔(𝒕),和一般的「黏滯阻尼」的SDOF系統之差異,主要是多了「摩擦力」(frictional force)
𝑭𝒔(𝒕),參閱圖示的EOM,說明如下:
1.
當速度為正值 𝒗 >𝟎,𝑭𝒔(𝒕)= −𝝁𝒎𝒈。
2.
當速度為負值 𝒗 <𝟎,𝑭𝒔(𝒕)= 𝝁𝒎𝒈。
3.
當速度為零 𝒗 =𝟎,𝑭𝒔(𝒕)= 0。
由於運動方程式EOM是二階的常微分方程式,所以,需要兩個「初始條件」(initial condition, IC),分別是「初始位移」𝒙𝟎及「初始速度」𝒗𝟎。【備註:比較明確的數學方程式,請讀者參考圖示,在文字說明,受限於方程式編寫,分別以𝒙、𝒗、𝒂,代表位移、速度、加速度。】
得到了系統的運動方程式EOM,對系統進行「模態分析」(modal analysis),可以求得結構的「模態參數」(modal parameters)。在此「單自由度系統」的「模態參數」為:
1. 𝒇𝒏=𝟏/𝟐𝝅 √(𝒌/𝒎):「自然頻率」(natural frequency),單位為 Hz。
2. 𝝎𝒏=𝟐𝝅𝒇𝒏:也是「自然頻率」(natural frequency),但是,單位為 rad/sec。
3. 𝝎𝒅=𝝎𝒏
√(𝟏−𝝃^𝟐 ):稱為「阻尼自然頻率」(damped natural frequency),單位為 rad/sec。
4. 𝝃=𝒄/C𝒄:為「阻尼比」(damping ratio),無因次單位。其中,C𝒄=2*(mk)^0.5=2mωn為「臨界黏滯阻尼係數」(critically viscous damping coefficient),單位為 N-s/m。
以上資訊,讀者可參考先前單元:#151,【「外力激振」的「單自由度系統」之振動分析】。
進行了「暫態響應分析」,就可以得到系統的時間域響應,有興趣的輸出參數,包括:
1. 質塊的時間波形響應:如位移𝒙(𝒕),速度 𝒗(𝒕),加速度 𝒂(𝒕)。
2. 相關的外力時間波形響應:如
𝑭𝒎𝒄𝒌(𝒕) = 𝑭𝒎(𝒕)+𝑭𝒄(𝒕)+𝑭𝒌(𝒕),分別是「慣性力」(inertial force) 𝑭𝒎(𝒕)=𝒎𝒂(𝒕),「阻尼力」(damping force) 𝑭𝒄(𝒕)= 𝒄𝒗(𝒕),「彈簧力」(spring force) 𝑭𝒌(𝒕)=
𝒌 𝒙(𝒕),而𝑭𝒎𝒄𝒌(𝒕)是3種系統力的合成。另外,「外力」(external force)
𝒇(𝒕)和「摩擦力」(frictional force)
𝑭𝒔(𝒕),都是有興趣的分析結果。同時,由EOM可以知道, 𝑭𝒎𝒄𝒌(𝒕) = 𝒇(𝒕)+𝑭𝒔(𝒕)。
接下來,以實際的數值分析案例作說明,設定:𝒎=1 (kg),𝒄=0 (N-s/m),𝒌=39.48 (N/m),則自然頻率
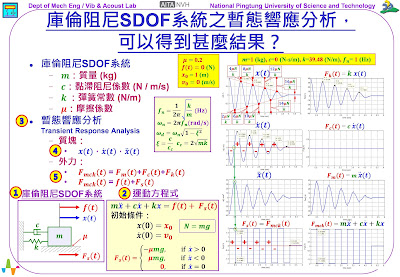
𝒇𝒏= 1 (Hz)。令𝒇(𝒕)=0,𝒙𝟎 = 1 (m),𝒗𝟎=𝟎 (m/s),而 𝝁=𝟎.2,所以是自由振動狀態。進行了「暫態響應分析」,就可以得到系統的時間域響應,針對質塊的時間波形響應:如位移𝒙(𝒕),速度 𝒗(𝒕),加速度 𝒂(𝒕),參閱圖示,其特徵說明如下:
1. 位移𝒙(𝒕):位移時間波形呈現振盪波動的衰減現象,其衰減率,以每半個波會下降2𝝁𝑵/𝒌,呈現「直線衰減」的現象。所以每一個波動會下降4𝝁𝑵/𝒌
的衰減量。因為有「庫倫摩擦」效應,最終,質塊會停留在略微偏移零點的位置。
2. 速度 𝒗(𝒕):速度𝒗(𝒕)和位移𝒙(𝒕),會有90度的相位角差異,也是有持續的振盪與衰減現象。
3. 加速度 𝒂(𝒕):加速度𝒂(𝒕)和位移𝒙(𝒕),則是有180度的相位角差異,也是有持續的振盪與衰減現象。比較特殊的是在最大和最小波峰處,會有突波(jump)效應,主要是來自摩擦力𝑭𝒔(𝒕)的影響。
除了質塊的時間波形響應外,也可以解析得到各種外力的時間波形響應,參閱圖示,其特徵說明如下:
1. 「彈簧力」(spring force) 𝑭𝒌(𝒕)=
𝒌 𝒙(𝒕):因為𝒌是常數,所以「彈簧力」𝑭𝒌(𝒕)和位移𝒙(𝒕)的特徵相同,只有彈簧常數𝒌的倍數差。
2. 「阻尼力」(damping force) 𝑭𝒄(𝒕)= 𝒄𝒗(𝒕):在本案例,𝒄=0 (N-s/m),所以「阻尼力」𝑭𝒄(𝒕)=0。
3. 「慣性力」(inertial force) 𝑭𝒎(𝒕)=𝒎𝒂(𝒕):因為𝒎是常數,所以「慣性力」𝑭𝒎(𝒕)和加速度 𝒂(𝒕)的特徵相同,只有質量𝒎的倍數差。
4. 𝑭𝒎𝒄𝒌(𝒕) = 𝑭𝒎(𝒕)+𝑭𝒄(𝒕)+𝑭𝒌(𝒕):𝑭𝒎𝒄𝒌(𝒕)是「慣性力」、「阻尼力」和「彈簧力」的合成力,其時間波形特徵和「摩擦力」𝑭𝒔(𝒕)完全相同。
5. 「摩擦力」(frictional force) 𝑭𝒔(𝒕):由EOM可以知道, 𝑭𝒎𝒄𝒌(𝒕) = 𝒇(𝒕)+𝑭𝒔(𝒕)。在本案例,沒有外力作用𝒇(𝒕)=0,所以,𝑭𝒎𝒄𝒌(𝒕) = 𝑭𝒔(𝒕)。值得注意的是,在質塊靜止的位置,仍有微小的「摩擦力」,如圖示,𝑭𝒔(𝒕=5)=0.01761
(N)。
另外,再看一下摩擦力𝑭𝒔(𝒕)與速度𝒗(𝒕)的關係,參閱圖示,有標示了
+ 和 − ,確實是當速度為正值 𝒗 >𝟎,𝑭𝒔(𝒕)= −𝝁𝒎𝒈為負值,當速度為負值
𝒗 <𝟎,𝑭𝒔(𝒕)= 𝝁𝒎𝒈為正值,而速度為零
𝒗 =𝟎,𝑭𝒔(𝒕)= 0。
由於摩擦力𝑭𝒔(𝒕)與速度𝒗(𝒕)呈現正負相反的關係,摩擦力𝑭𝒔(𝒕)又與「摩擦係數」𝝁成正比,所以,會有抑制振動的「庫倫阻尼」衰減效應。因此,「摩擦係數」𝝁逐漸增大,質塊振盪的衰減效應越快。
其次,在加速度 𝒂(𝒕)的時間波形,有突波(jump)效應,可以發現都是出現在速度 𝒗(𝒕)的正負值交錯區間,同時也是摩擦力𝑭𝒔(𝒕)的負正交錯區間,進而形成了此突波(jump)效應。
最後,綜合一下這個單元的討論重點:
1. 瞭解了「庫倫阻尼」(Coulomb Damping) SDOF系統:系統參數包括:𝒎=質量 (kg),𝒄=黏滯阻尼係數 (N / m/s),𝒌=彈簧常數 (N/m),𝝁=摩擦係數。
2. 推導得到「庫倫阻尼」SDOF系統的運動方程式(Equation of Motion, EOM):通式如下:𝒎𝒂+𝒄𝒗+𝒌𝒙=𝒇(𝒕)+𝑭𝒔(𝒕)。
3. 瞭解了「暫態響應分析」(Transient Response Analysis):主要目的就是要分析取得系統的時間域響應。
4. 探討了質塊的時間波形響應特徵:如位移𝒙(𝒕),速度 𝒗(𝒕),加速度 𝒂(𝒕)。
5. 也探討了系統的各種外力之時間波形響應特徵:如𝑭𝒎𝒄𝒌(𝒕) = 𝑭𝒎(𝒕)+𝑭𝒄(𝒕)+𝑭𝒌(𝒕) = 𝒇(𝒕)+𝑭𝒔(𝒕)。
以上個人看法,請多指教!
王栢村














0 意見:
張貼留言