這個單元是SDOF簡諧激振FRF系列的第6篇,要來探討的主題是:「彈簧常數」(spring constant)增大或減小,對「頻率響應函數」(Frequency Response Function, FRF)有甚麼影響?
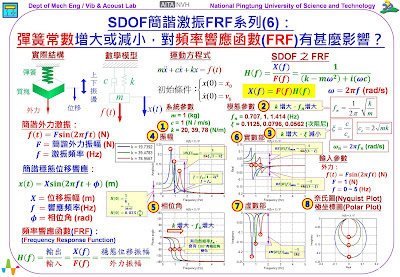
首先,快速回顧一下這個「外力激振」「單自由度系統」,參考圖示左上方,是實際結構的示意圖,一個質塊,懸吊在一個彈簧下面,彈簧的另一端是固定邊界,當質塊受到外力作用,質塊會有上下振盪的現象。
為了分析這個質塊-彈簧的「實際結構」(real structure),建構此系統「數學模型」(mathematical model),如示意圖。其中,
1.
「系統參數」(system parameters),就是:m、c、k,分別是質塊的「質量」(mass)、彈簧的「黏滯阻尼係數」(viscous damping coefficient)、彈簧的「彈簧常數」(spring constant)。
2.
「輸入」是f(t),為系統的外力,以及質塊本身的兩個「初始條件」(initial condition, IC),包括:「初始位移」(initial displacement) X0及「初始速度」(initial velocity) V0。
3.
「輸出」是x(t),為系統質塊的位移響應。
由系統的「數學模型」,可以推導出這個「單自由度系統」的「運動方程式」:ma+cv+kx=f(t)。是「二階的常微分方程式」,所以需要兩個「初始條件」:「初始位移」X0及「初始速度」V0。【備註:比較明確的數學方程式,請讀者參考圖示,在文字說明,受限於方程式編寫,分別以x、v、a,代表位移、速度、加速度。】
接著,定義系統的「輸入參數」,假設系統受到了「簡諧外力」激振,為正弦函數
𝒇(𝒕)=𝑭𝐬𝐢𝐧(𝟐𝝅𝒇𝒕),其中,𝑭 =「簡諧外力振幅」;𝒇=「簡諧外力」的「激振頻率」。
當這個正弦波的「簡諧外力」,作用在此「SDOF單自由度系統」,由先前單元:#208,【SDOF簡諧激振系列(2):為甚麼簡諧激振,會有簡諧響應?】,質塊的位移響應𝒙(𝒕),可以區別出,有「暫態響應」(transient state response),以及「穩態響應」(steady state response)的區間。
其中,有興趣的是「穩態位移響應」,也是「簡諧響應」,可以寫出位移響應方程式:𝒙(𝒕)=𝑿𝐬𝐢𝐧(𝟐𝝅𝒇𝒕+𝝓),其中,
1. 𝑿:是「穩態位移響應」的「位移振幅」。
2. 𝒇:是「穩態位移響應」的「響應頻率」,此頻率值就是「簡諧外力」的「激振頻率」。
3. 𝝓:是「穩態位移響應」的「相位角」(phase
angle),是「位移」𝒙(𝒕)和「外力」𝒇(𝒕)的「相位角」差。
特別有興趣的是「位移振幅」𝑿 和「相位角」𝝓。為了有效率的全盤了解「穩態位移響應」的特性,所以,定義了「頻率響應函數」(Frequency Response Function, FRF),𝑯(𝒇):
1.
𝑯(𝒇) = 輸出/輸入。
2.
𝑯(𝒇) =
𝑿(𝒇)/𝑭(𝒇)。
3.
𝑯(𝒇) =「穩態位移振幅」/「外力振幅」。
這樣,可以快速知道𝑿(𝒇)和𝑭(𝒇)的關係。又,因為不同的「激振頻率」𝒇,會有不同的「穩態位移振幅」𝑿,所以,分別以𝑿(𝒇)和𝑭(𝒇)變數符號表示之。
針對「單自由度系統」之 FRF:𝑯(𝒇) = 𝑿(𝒇)/𝑭(𝒇) = 𝟏/[(𝒌−𝒎𝝎^𝟐 )+𝒊(𝝎𝒄)],會和「系統參數」:m、c、k相關,也會隨著不同的「激振頻率」𝒇,而會有不同的𝑯(𝒇)。
首先,由FRF定義:𝑯(𝒇) = 𝑿(𝒇)/𝑭(𝒇),可以推導出來,𝑿(𝒇) = 𝑭(𝒇)
𝑯(𝒇)。也就是說,如果知道系統的m、c、k,就可以求得「頻率響應函數」𝑯(𝒇),當已知「簡諧外力」的「外力振幅」𝑭,以及其「激振頻率」𝒇,就可以透過上面的方程式,推算出「穩態位移響應」𝑿(𝒇),包括:「位移振幅」𝑿和「相位角」𝝓。
這個單元要來探討:「彈簧常數」(spring constant)增大或減小,對「頻率響應函數」(Frequency Response Function, FRF)有甚麼影響?
在此,列舉的實際數值案例,令「系統參數」:m = 1 (kg)、c =
1 (N/ m/s)、k = 19.73, 39.47, 78.95
(N/m),也就是m及c固定,變動不同的k =
19.73, 39.47, 78.95 (N/m)。
由「系統參數」:m、c、k,可以推算得到「模態參數」:「自然頻率」𝒇𝒏 = 0.707, 1, 1.414 (Hz),「阻尼比」𝝃 = 0.1125, 0.0796,
0.0562。因為,0 < 𝝃 < 1,所以都是「次阻尼」狀態。可以知道:變動不同的m
= 0.5, 1, 2 (kg),「模態參數」的變化特徵:
1. k增大,𝒇𝒏增大。因為:「自然頻率」和「彈簧常數」的倒數開根號成正比。
2. k增大,𝝃減小。因為:「阻尼比」和「彈簧常數」的倒數開根號成反比。
接著,假設「簡諧外力」激振:𝒇(𝒕)=𝑭𝐬𝐢𝐧(𝟐𝝅𝒇𝒕),其中,「簡諧外力振幅」𝑭 =1 (N);「簡諧外力」的「激振頻率」𝒇=0~5 (Hz)。
將已知的「系統參數」:m、c、k,帶入「單自由度系統」之 FRF方程式,並畫出𝑯(𝒇)的5種圖示,包括:(1)「振幅」(amplitude)、(2)「相位角」(phase angle)、(3)「實數部」(real)、(4)「虛數部」(imaginary)、以及(5)「奈氏圖」(Nyquist plot),或稱為「極坐標圖」(polar plot)。
以下就針對𝑯(𝒇)的5種圖示,在固定m及c,而變動不同的k =
19.73, 39.47, 78.95 (N/m)時,來觀察有甚麼特徵與差異:
1. 「振幅」(amplitude):FRF曲線的「峰值」(peak),有最大的位移響應,對應的頻率就是「自然頻率」𝒇𝒏。當k增大,𝒇𝒏增大,所以「峰值」就向右偏移。實務上,因為「阻尼比」𝝃都很小,出現「峰值」的頻率點,參閱圖示的方程式,可知,會是𝒇≈𝒇𝒏。另外,在「峰值」頻率的振幅值,可參閱圖示的方程式,可知:k增大,其振幅值會越小。在此,也可觀察:因為,k增大,所以,「峰值」頻率的振幅值,也減小。另外,一個重要特徵,當𝒇=0時,𝑯(0) =1/k,在此,因為k值不同,所以,𝑯(0)也會不同。
2. 「相位角」(phase angle):有「自然頻率」𝒇𝒏的頻率附近,會有𝝓 =180°的「相位角」變化。在𝒇=𝒇𝒏時,𝝓 =90°。又,𝒇<𝒇𝒏時,𝝓≈0°,是「同相」(in phase)。在 𝒇>𝒇𝒏時,𝝓≈180°,是「反相」(out-of-phase)。
3. 「實數部」(real):「自然頻率」𝒇𝒏會出現在,通過「0點」的頻率。參閱圖示中的方程式,可以知道:因為,k增大,所以,「峰值」頻率所對應的振幅值減小。
4. 「虛數部」(imaginary):「自然頻率」𝒇𝒏會出現在,有最大「峰值」的頻率。參閱圖示中的方程式,可以知道:因為,k增大,所以,「峰值」頻率所對應的振幅值減小。
5. 「奈氏圖」(Nyquist plot),或稱為「極坐標圖」(polar plot):會形成一個「圓圈」,在「虛數部」最大值的頻率點,就是結構的「自然頻率」。因為,k增大,所以,「峰值」頻率所對應的「虛數部」振幅值減小,因此,「圓圈」會有較小的直徑。有一個模態,就會形成一個「圓圈」,所以,在多自由度系統時,FRF的「奈氏圖」就會形成多個「圓圈」。
綜合一下這個單元的討論重點:「彈簧常數」(spring constant)增大或減小,對「頻率響應函數」(Frequency Response Function, FRF)有甚麼影響?統整如下:
1.
令「系統參數」:m及c固定,變動不同的k =
19.73, 39.47, 78.95 (N/m)。
2.
k增大,𝒇𝒏增大。
3.
k增大,𝝃減小。
4.
「振幅」(amplitude)圖:因為,k增大,𝒇𝒏增大,所以「峰值」就是「自然頻率」𝒇𝒏,會向右偏移。同時,「峰值」的振幅值𝑯(𝒇𝒏),也會因為k增大,而振幅值𝑯(𝒇𝒏)隨著減小。
5.
「相位角」(phase angle)圖:在「自然頻率」𝒇𝒏的頻率附近,會有𝝓 =180°的「相位角」變化。在𝒇=𝒇𝒏時,𝝓 =90°。在𝒇<𝒇𝒏時,𝝓≈0°,是「同相」(in phase)。在 𝒇>𝒇𝒏時,𝝓≈180°,是「反相」(out-of-phase)。
6.
「實數部」(real)圖:通過「0點」的頻率,會是「自然頻率」𝒇𝒏。「峰值」頻率所對應的振幅值,會隨著k增大,而減小。
7.
「虛數部」(imaginary):有最大「峰值」的頻率,會是「自然頻率」𝒇𝒏。「峰值」頻率所對應的振幅值,會隨著k增大,而減小。
8.
「奈氏圖」(Nyquist plot),或稱為「極坐標圖」(polar plot):會形成一個「圓圈」,在「虛數部」最大值的頻率點,就是結構的「自然頻率」。因為,k增大,所以,「圓圈」的直徑也會減小。
以上個人看法,請多指教!
王栢村
2021.05.14
YouTube影片連結
訂閱電子報














0 意見:
張貼留言