這個單元要來探討的主題是:如何建構「離散系統」(discrete system)的「數學模型」(mathematical model)?-
以【搖頭娃娃】為例。
要進行一個結構的「振動分析」(vibration analysis),建構「數學模型」(mathematical model)是一個重要步驟,稱為「數學建模」(mathematical modeling)。也就是將「實際結構」(real structure)做適當的假設,以能夠得到對應於「實際結構」的等效「數學模型」(mathematical model)。
參考先前單元:#312,【如何進行一個結構系統的振動分析?】,首先快速回顧一下,典型之振動問題解析流程,可以歸納如下幾個步驟:
1. 工程問題描述(problem description):
2. 定義問題(define problem)及擬定分析目標(analysis objectives):
3. 建構「數學模型」(mathematical model) =「數學建模」(mathematical modeling):
4. 分析:
5. 結果討論與評估:
6. 報告:
可參閱圖1,左側列出詳細的步驟說明:
1. 工程問題描述(problem description):建議採用:【4個What】的心法,(1) What to know? 想要知道甚麼?(2) What to get? 需要得到甚麼?(3) What to do? 必須做甚麼?(4) What to show? 應該呈現甚麼?
2. 定義問題(define problem)及擬定分析目標(analysis objectives):在定義問題(define problem),建議採用的心法:ISO / SPR / FGMBIR。分別是:(1) Input →
System →
Output、(2) Source →
Path →
Response、(3) Force →
GMBI →
Response。
3. 建構「數學模型」(mathematical model):「數學模型」可以概分為兩種:(1)「離散系統」(discrete system)和
(2)「連續系統」(continuous system)。參閱圖1右上方圖示,(1)「離散系統」(discrete system):一種「數學模型」,假設結構是「剛體」(rigid body),所以,會是具有”有限個”自由度(“finite” degree-of-freedom, DOF)。(2) 「連續系統」(continuous system):另一種「數學模型」,假設結構是「撓性體」(flexible body),或稱為「彈性體」(elastic body),所以會有”無限多個”自由度(“infinite” degree-of-freedom,
DOF)。
4. 分析:進行對應的分析,主要的分析類型,包括:(1)「模態分析」(modal analysis),(2)「簡諧響應分析」(harmonic response analysis),(3) 「暫態響應分析」(transient response analysis),(4)「頻譜響應分析」(spectrum response analysis)。
5. 結果討論與評估:針對分析結果,提出對應的討論與評估,重點在評估是否能夠解答問題描述的想要知道甚麼?
6. 報告:撰寫報告,不外是書面報告(documentation),以及必要的口頭報告(oral presentation)。
這個單元著重在討論:如何建構「數學模型」(mathematical model)?也就是「數學建模」(mathematical modeling)的步驟。進行「數學建模」的重要目標,在取得合理性(Reasonable)、正確性(Correct)、適宜性(Adaptation)的「數學模型」,是後續振動模擬分析成功與否之關鍵!
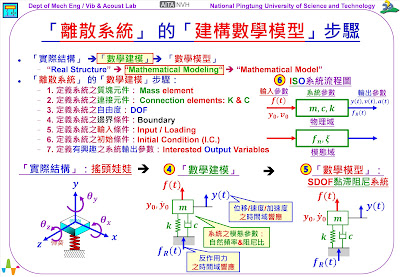
這個單元,將以「離散系統」(discrete system),探討說明建構「數學模型」(mathematical model)的7個步驟,包括:
1. 定義系統之質塊元件:
2. 定義系統之連接元件:
3. 定義系統之自由度:
4. 定義系統之邊界條件:
5. 定義系統之輸入條件:
6. 定義系統之初始條件:
7. 定義有興趣之系統輸出參數:
參閱圖2,是「離散系統」的「數學建模」步驟。「數學建模」主要目的,在對「實際結構」(real structure)做適當的假設,進行「數學建模」(mathematical modeling),以能得到對應「實際結構」的「數學模型」(mathematical model)。在此以【搖頭娃娃】為例做說明。
首先觀察圖2,左下方是「實際結構」:【搖頭娃娃】,其主要結構就是一個質塊與彈簧,【搖頭娃娃】受到敲擊、或拉扯後,娃娃頭的質塊會有跳動情形。所以,質塊會有3個方向位移/平移「自由度」:𝒙,𝒚,𝒛,以及3個方向旋轉「自由度」:𝜽𝒙,𝜽𝒚,𝜽𝒛。
在此,希望建構一個適當的「數學模型」,以能夠模擬分析這個【搖頭娃娃】的運動狀態。所以就要進行「數學建模」,依照建議的步驟,逐項說明如下:
1. 定義系統之質塊元件:就是Mass element。以一個質量塊𝒎,代表【搖頭娃娃】的質塊。
2. 定義系統之連接元件:就是Connection elements,K & C。也就是分別以一個彈簧常數𝒌和黏滯阻尼係數𝒄,代表【搖頭娃娃】的垂直方向彈簧效應。因為,主要的振動在垂直方向。
3. 定義系統之自由度:就是Degree-of-Freedom (DOF)。雖然質量塊𝒎有6個自由度,但是,在連接元件,只定義了垂直方向的彈簧效應,所以,只需考慮此系統的垂直方向的位移,也就是「自由度」𝒚(𝒕)。
4. 定義系統之邊界條件:就是Boundary。如圖示的基座是固定的。
5. 定義系統之輸入條件:就是Input或Loading。可以合理定義作用在質量塊𝒎上的垂直方向外力是
𝒇(𝒕)。
6. 定義系統之初始條件:就是Initial Condition (I.C.)。必須要定義「自由度」𝒚(𝒕) 的I.C.,包括:初始位移𝒚𝟎和初始速度𝒚 ̇𝟎。
7. 定義有興趣之系統輸出參數:就是Interested Output Variables。(1)系統之模態參數:自然頻率𝒇𝒏&阻尼比𝝃。(2)位移/速度/加速度之時間域響應
𝒚(𝒕) , 𝒗(𝒕), 𝒂(𝒕)。(3)反作用力之時間域響應𝒇𝑹(𝒕)。
完成了以上「數學建模」的7個步驟,可以得到如圖2右下方的【搖頭娃娃】之「數學模型」,是一個「SDOF黏滯阻尼系統」。
也可以由【ISO系統流程圖】來觀察「數學模型」,參閱圖2右上方圖示,ISO的說明如下:
1. Input variables 輸入參數:包括:外力 𝒇(𝒕)。以及I.C.,包括:初始位移𝒚𝟎和初始速度𝒚 ̇𝟎。
2. System variables 系統參數:包括:質量塊𝒎,黏滯阻尼係數𝒄和彈簧常數𝒌。
3. Output variables 輸出參數:包括:「自由度」響應 𝒚(𝒕), 𝒗(𝒕), 𝒂(𝒕)。反作用力𝒇𝑹(𝒕)。
以上所列出的參數,都是物理參數(physical parameters),都是可以度量的物理量(physical quantity),所以稱此流程圖是:物理域(physical domain)的【ISO系統流程圖】。
另外,也可以畫出模態域(modal domain)的【ISO系統流程圖】,其中,系統參數是自然頻率𝒇𝒏&阻尼比𝝃。
綜合一下這個單元的討論,為了探討如何建構「離散系統」(discrete system)的「數學模型」(mathematical model)?重點摘要如下:
1. 典型之振動問題解析流程,可以歸納出6個步驟。
2. 建構「數學模型」(mathematical model)。「數學模型」可以區分為:(1)「離散系統」(discrete system)。(2) 「連續系統」(continuous system)。
3. 針對「離散系統」(discrete system)的「數學建模」(mathematical modeling),有7個步驟。
4. 以【搖頭娃娃】為例,說明「數學建模」的完整流程步驟。
5. 可以得到了【搖頭娃娃】的「數學模型」,是一個「SDOF黏滯阻尼系統」。
6. 最後,介紹了物理域(physical domain)和模態域(modal domain)的【ISO系統流程圖】
以上個人看法,請多指教!
王栢村















0 意見:
張貼留言