這個單元要來探討的主題是:如何檢查「頻譜分析儀」(FFT spectrum Analyzer)的基本功能(basic functions)正常運作?這是這個系列的第7篇,針對第3項的功能檢查:3. 自身功率頻譜密度檢查(Auto PSD Spectrum Check)。
本單元在探討由「時間波形」(time waveform)與「自身功率頻譜」(Auto PSD Spectrum),所取得的平方平均根值(root mean square value, 𝒓𝒎𝒔 value),或簡稱方均根值,也就是𝒓𝒎𝒔值。藉由兩者之間的比較,來驗證自身功率頻譜密度的功能檢查。
首先,回顧前一個單元:#379,【如何檢查頻譜分析儀(FFT
spectrum analyzer) – 3.自身功率頻譜密度檢查(Auto
PSD Spectrum Check) – 原理(Principle)】,參閱圖1,簡要回顧說明如下:
1. 回顧先前單元:#338,【如何進行EMA量測數據之信號處理?】,參閱圖1右上方,EMA量測數據之信號處理流程圖,從「時間波形」(time waveform),進行FFT分析,取得「傅立葉頻譜」(Fourier spectrum),再透過PSD分析,可以取得「功率頻譜密度」(Power Spectral Density, PSD)函數,進而由FRF分析,可以得到「頻率響應函數」(frequency response function, FRF)以及「關聯性函數」(coherence, COH)。本單元重點在:PSD分析的基本原理。
2. 以【4W】的心法:(1) What is? 甚麼是PSD spectrum「功率頻譜」?(2) Why to do?
為什麼要取得PSD spectrum「功率頻譜」?(3) What goal?
取得PSD spectrum「功率頻譜」要達到甚麼目標?(4) 如何取得PSD spectrum「功率頻譜」?做了概述探討。包括:「自身功率頻譜」(Auto PSD)以及「交叉功率頻譜」(Cross PSD)。
3. 針對Auto PSD以及Cross PSD,分別由數位化的「傅立葉頻譜」定義其計算與分析方式。
4. 特別對Auto PSD,說明𝑮𝒖𝒖(𝒇) PSD spectrum「功率頻譜」不同單位的表示方式。最重要的Auto PSD單位,是𝑼𝐫𝐦𝐬^𝟐/𝐇𝐳。
5. 典型的𝑮𝒖𝒖(𝒇) PSD spectrum,例如:外力的Auto PSD,𝑮𝒇𝒇(𝒇)單位= (𝑵 𝐫𝐦𝐬^𝟐)/𝐇𝐳。加速度的Auto PSD, 𝑮𝒂𝒂(𝒇)單位= (g
𝐫𝐦𝐬^𝟐)/𝐇𝐳。
6. 一個信號的𝒓𝒎𝒔值,可以由𝑮𝒖𝒖(𝒇) PSD spectrum「功率頻譜」曲線,透過積分式,取得𝑼𝐫𝐦𝐬,𝒇。
7. 一個信號的𝒓𝒎𝒔值,也可以直接由𝒖(𝒕)「時間波形」的原始量測數據,求得𝑼𝐫𝐦𝐬,𝒕。
8. 如果,由𝑮𝒖𝒖(𝒇) PSD spectrum「功率頻譜」曲線取得的𝑼𝐫𝐦𝐬,𝒇,和由𝒖(𝒕)「時間波形」的原始量測數據求得的𝑼𝐫𝐦𝐬,𝒕,兩者相等:𝑼𝐫𝐦𝐬,𝒇 =
𝑼𝐫𝐦𝐬,𝒕,就可以驗證計算取得的𝑮𝒖𝒖(𝒇) PSD spectrum「功率頻譜」之正確性。盡管是以Auto PSD,進行驗證分析,因為Cross PSD和Auto PSD算法相同,所以,可以校正PSD分析的正確性。
參閱圖2,分別是常數波(constant)、餘弦波(cosine)、正弦波(sine)、以及三者合成信號之𝒓𝒎𝒔值的數值計算驗證比較結果,最下方是計算原理的方程式,包括:(1) Auto PSD頻譜、(2) 平方平均根RMS–時間波形、(3) 平方平均根RMS–Auto PSD頻譜。
圖2的第一列圖示是「傅立葉頻譜」(Fourier spectrum),而第二列圖示是「自身功率頻譜」(Auto PSD),比較探討說明如下:
1. 常數波(constant):令:𝒙𝟏 (𝒕)=𝑨𝟏,𝑨𝟏=𝟓,𝒇𝟏=𝟎 Hz,由「時間波形」,可得到:𝒙𝟏,𝒓𝒎𝒔,𝒕 =𝟓。其「傅立葉頻譜」𝑼(𝒇=𝟎) =
𝟓,可據以求得其「自身功率頻譜」,𝑮𝒖𝒖 (𝒇=𝟎)=𝟓𝟎,而由𝑮𝒖𝒖 (𝒇)計算得到的𝒓𝒎𝒔值,也是𝒙𝟏,𝒓𝒎𝒔,𝒇 =𝟓。所以,𝒙𝟏,𝒓𝒎𝒔,𝒕 =
𝒙𝟏,𝒓𝒎𝒔,𝒇 =𝟓。
2. 餘弦波(cosine):令:𝒙𝟐 (𝒕)=𝑨𝟐 𝐜𝐨𝐬(𝟐𝛑𝒇𝟐 𝒕),𝑨𝟐=2,𝒇𝟐=𝟏𝟎𝟎 Hz,由「時間波形」,可得到:𝒙𝟐,𝒓𝒎𝒔,𝒕 =𝟏.𝟒𝟏𝟒。其「傅立葉頻譜」之實數部,𝑼(𝒇=
𝟏𝟎𝟎) = 𝟐,可據以求得其「自身功率頻譜」,𝑮𝒖𝒖 (𝒇=
𝟏𝟎𝟎)= 8,而由𝑮𝒖𝒖 (𝒇)計算得到的𝒓𝒎𝒔值,也是𝒙𝟐,𝒓𝒎𝒔,𝒇 =
𝟏.𝟒𝟏𝟒。所以,𝒙𝟐,𝒓𝒎𝒔,𝒕 =
𝒙𝟐,𝒓𝒎𝒔,𝒇 =
𝟏.𝟒𝟏𝟒。
3. 正弦波(sine):令:𝒙𝟑 (𝒕)=𝑨𝟑 𝐬𝐢𝐧(𝟐𝛑𝒇𝟑 𝒕),𝑨𝟑=𝟏𝟎,𝒇𝟑=𝟐𝟓𝟎 Hz,由「時間波形」,可得到:𝒙𝟑,𝒓𝒎𝒔,𝒕 =𝟕.𝟎𝟕𝟏。其「傅立葉頻譜」之虛數部,𝑼(𝒇=
𝟐𝟓𝟎) =–𝟏𝟎,可據以求得其「自身功率頻譜」,𝑮𝒖𝒖 (𝒇=
𝟐𝟓𝟎)= 𝟐𝟎𝟎,而由𝑮𝒖𝒖 (𝒇)計算得到的𝒓𝒎𝒔值,也是𝒙𝟑,𝒓𝒎𝒔,𝒇 =
𝟕.𝟎𝟕𝟏。所以,𝒙𝟑,𝒓𝒎𝒔,𝒕 =
𝒙𝟑,𝒓𝒎𝒔,𝒇 =
𝟕.𝟎𝟕𝟏。
4. 三者合成信號:令:𝒙(𝒕)=𝒙𝟏 (𝒕)+𝒙𝟐 (𝒕)+𝒙𝟑 (𝒕),由「時間波形」,可得到:𝒙,𝒓𝒎𝒔,𝒕 =8.75𝟓。其「傅立葉頻譜」之振幅值,如預期,𝑼(𝒇=𝟎) =
𝟓,𝑼(𝒇=
𝟏𝟎𝟎) = 𝟐,𝑼(𝒇=
𝟐𝟓𝟎) =𝟏𝟎。可據以求得其「自身功率頻譜」,𝑮𝒖𝒖 (𝒇=𝟎)=𝟓𝟎,𝑮𝒖𝒖 (𝒇=
𝟏𝟎𝟎)= 8,𝑮𝒖𝒖 (𝒇=
𝟐𝟓𝟎)= 𝟐𝟎𝟎。而由𝑮𝒖𝒖 (𝒇)計算得到的𝒓𝒎𝒔值,也是𝒙,𝒓𝒎𝒔,𝒇 =8.75𝟓。所以,𝒙,𝒓𝒎𝒔,𝒕 =
𝒙,𝒓𝒎𝒔,𝒇 =
8.75𝟓。
由以上單一的常數波(constant)、餘弦波(cosine)、正弦波(sine),以及三者合成信號之𝒓𝒎𝒔值的計算驗證比較,由「時間波形」得到的𝒓𝒎𝒔值,與由「自身功率頻譜」得到的𝒓𝒎𝒔值,兩兩相同,因此,可以驗證「自身功率頻譜」之程式演算法的正確性。
回顧一下這個單元的討論:
1. 主要的驗證原理,是觀察由「時間波形」得到的𝒓𝒎𝒔值,與由「自身功率頻譜」得到的𝒓𝒎𝒔值,兩兩相同。
2. 分別透過:(1)常數波(constant)、(2)餘弦波(cosine)、(3)正弦波(sine)、以及(4)三者合成信號之𝒓𝒎𝒔值的計算驗證比較,確認了數值比較驗證,符合𝒙,𝒓𝒎𝒔,𝒕 =
𝒙,𝒓𝒎𝒔,𝒇,基本特性。
3. 因此,可以佐證「自身功率頻譜」(Auto PSD)的程式算法,正確無誤。進而,可以應用到求得「交叉功率頻譜」(Cross PSD)。
以上個人看法,請多指教!
王栢村
2024.07.22
 |
圖1、自身功率密度頻譜檢查(Auto PSD Spectrum Check) – 原理(Principle) |
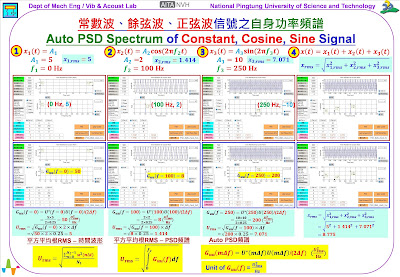 |
圖2、常數波、餘弦波、正弦波信號之自身功率頻譜 |














0 意見:
張貼留言